Ισομέρεια είναι το φαινόμενο όπου δύο ενώσεις έχουν τον ίδιο μοριακό τύπο αλλά διαφορετικές ιδιότητες.
Ένα παράδειγμα του φαινομένου είναι η θεοβρωμίνη, συστατικό της σοκολάτας και η θεοφυλλίνη, φάρμακο για το άσθμα.
Ή ακόμα η διαφορά στις ιδιότητες, μπορεί και να οφείλεται σε διαφορετική διάταξη των ατόμων στο χώρο, όπως ο τρόπος που είναι συνδεδεμένα τα πέντε μας δάχτυλα στις παλάμες μας. Ίδια σύνδεση αλλά διαφορετική διάταξη, και γι' αυτό το δεξί γάντι δεν μπαίνει στο αριστερό χέρι.
Αλκάνια είναι οι οργανικές ενώσεις που αποτελούνται μόνο από άνθρακα και υδρογόνο, υδρογονάνθρακες, και δεν έχουν κανένα πολλαπλό δεσμό. Είναι οι απλούστερες οργανικές ενώσεις και βρίσκονται στο πετρέλαιο.
Αν έχουμε τρία μόνο άτομα άνθρακα προφανώς έχουμε μόνο έναν τρόπο να τα συνδέσουμε μεταξύ τους. Να τα βάλουμε στη σειρά. Έτσι αφού προσθέσουμε και τα απαραίτητα υδρογόνα (οκτώ) θα έχουμε μόνο ένα αλκάνιο το προπάνιο.
Αν έχουμε τέσσερα άτομα άνθρακα έχουμε δύο τρόπους να τα συνδέσουμε. είτε να τα βάλουμε στην ευθεία, είτε να σχηματίσουμε ένα ταφ (Τ). Δηλαδή θα έχουμε δύο διαφορετικά-ισομερή αλκάνια. Το n-βουτάνιο και το ισοβουτάνιο (μέθυλο προπάνιο).
Με πέντε άτομα έχουμε τρεις διαφορετικές διατάξεις:
Αν ενδιαφέρεστε για μέχρι τους 60 άνθρακες θα τα βρείτε εδώ: https://oeis.org/A000602/b000602.txt επίσης από τον N. J. A. Sloane
Και τέλος στη σελίδα https://oeis.org/A000602/a000602_1.txt μπορείτε να βρείτε ένα πρόγραμμα για τον υπολογιστή σας, από τον Jean-François Alcover, που σας δίνει αυτές τις ακολουθίες. Το πρόγραμμα είναι γραμμένο στη γλώσσα mathematica (γλώσσα μαθηματικών από το MIT) και μπορείτε να το εκτελέσετε στο cloud από εδώ: http://develop.open.wolframcloud.com/app/
Πηγή: "On-Line Encyclopedia of Integer Sequences"
Ένα παράδειγμα του φαινομένου είναι η θεοβρωμίνη, συστατικό της σοκολάτας και η θεοφυλλίνη, φάρμακο για το άσθμα.
 |
Θεοβρωμίνη επίσης γνωστή και ως ξανθόζη,
ένα αλκαλοειδές που βρίσκεται στη σοκολάτα.
Υπό: Jynto - Own work,
CC0, Wikimedia Commons |
 Θεοφυλλίνη επίσης γνωστή σαν διμεθυλξανθίνη, ένα φάρμακο για ασθένειες του αναπνευστικού. Υπό Jynto - Own work, CC0, Wikimedia Commons |
Και οι δυο ενώσεις έχουν τον ίδιο μοριακό τύπο C7H8N4O2. Επτά άνθρακες (μαύρες σφαίρες) τέσσερα άζωτα (μπλε σφαίρες) δύο οξυγόνα (κόκκινες σφαίρες) και οκτώ υδρογόνα (λευκές σφαίρες). Η διαφορά τους οφείλεται στη διαφορετική θέση του μεθυλίου (-CΗ3), που στην μεν θεοβρωμίνη βρίσκεται επάνω δεξιά ενώ στη θεοφυλλίνη επάνω αριστερά.
Αυτή η διαφορά οφείλεται στον διαφορετικό τρόπο σύνδεσης των ατόμων.
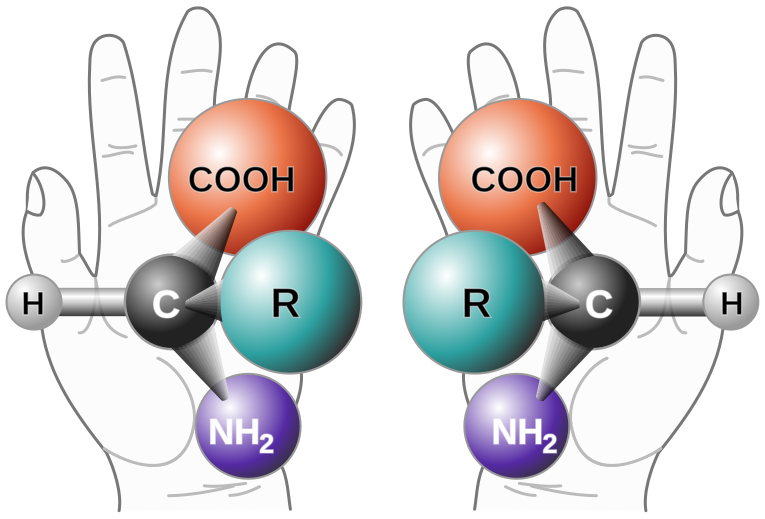 |
| Δύο εναντιομερή της γενικής μορφής των αμινοξέων που είναι χειρόμορφα.
Η χειρομορφία των αμινοξέων. "Χειρόμορφο" είναι ένα μόριο που δεν ταυτίζεται με το κατοπτρικό του είδωλο. Όπως το αριστερό και το δεξιό χέρι που έχουν τον αντίχειρα, και τα δάχτυλα με την ίδια σειρά (δείκτης, μέσος. παράμεσος, μικρός), αλλά το ένα είναι είναι κατοπτρικό είδωλα του άλλου. και όχι ίδια. Αν δούμε στον καθρέφτη το δεξ'ι μας χέρι νομίζουμε ότι είναι το αριστερό. Έτσι και τα χειρόμορφα μόρια έχουν τα ίδια πράγματα (άτομα ομάδες) συνδεδεμένα με την ίδια σειρά, αλλά είναι είδωλα σε καθρέφτη και όχι τα ίδια. Αν και τα περισσότερα αμινοξέα μπορούν να υπάρχουν και στις δύο μορφές αριστερή και δεξιά, η Ζωή στη Γη είναι κατασκευασμένη από αριστερόμορφα αμινοξέα, σχεδόν αποκλειστικά. Κανείς δεν ξέρει γιατί συμβαίνει αυτό. Ωστόσο, οι Δρ. Ο John Cronin και η Sandra Pizzarello έχουν δείξει ότι μερικά από τα αμινοξέα που πέφτουν στη γη από το διάστημα είναι περισσότερο αριστερά από δεξιά. Έτσι, το γεγονός ότι είμαστε κατασκευασμένοι από αμινοξέα L(left-αριστερόμορφα) μπορεί να οφείλεται σε αμινοξέα από το διάστημα.
Γιατί τα αμινοξέα στο διάστημα ευνοούν το L; Κανείς δεν ξέρει πραγματικά, αλλά είναι γνωστό ότι η ακτινοβολία μπορεί επίσης να υπάρχει σε μορφές αριστερόστροφη και δεξιόστροφη. Έτσι, υπάρχει μια θεωρία που ονομάζεται υπόθεση Bonner, η οποία προτείνει ότι η αριστερόστροφη ακτινοβολία στο διάστημα (από ένα περιστρεφόμενο αστέρι νετρονίων, για παράδειγμα) θα μπορούσε να οδηγήσει σε αριστερόχειρα αμινοξέα στο διάστημα, γεγονός που θα εξηγούσε τα αριστερόχειρα αμινοξέα σε μετεωρίτες. Αυτό είναι ακόμα εικασίες, αλλά η έρευνα το καθιστά πολύ πιό εύλογο.
Υπό: - πϵρήλιο ℗ - Public Domain, Wikimedia Commons
|
Και πόσα είναι τα ισομερή ενός αλκανίου.
Στην οργανική χημεία το φαινόμενο της ισομέρειας συνεισφέρει στον τεράστιο αριθμό των οργανικών ενώσεων. Ας περιοριστούμε μόνο στον διαφορετικό τρόπο σύνδεσης, η οποία μάλιστα λέγεται συντακτική ισομέρεια. Η άλλη περίπτωση, αυτή στο χώρο, λέγεται στερεοισομέρεια. |
| Φυσική πηγή πετρελαίου στην Korňa, Slovakia By PetrS. - Own work, CC BY-SA 3.0, Wikimedia Commons |
Αν έχουμε τρία μόνο άτομα άνθρακα προφανώς έχουμε μόνο έναν τρόπο να τα συνδέσουμε μεταξύ τους. Να τα βάλουμε στη σειρά. Έτσι αφού προσθέσουμε και τα απαραίτητα υδρογόνα (οκτώ) θα έχουμε μόνο ένα αλκάνιο το προπάνιο.
Αν έχουμε τέσσερα άτομα άνθρακα έχουμε δύο τρόπους να τα συνδέσουμε. είτε να τα βάλουμε στην ευθεία, είτε να σχηματίσουμε ένα ταφ (Τ). Δηλαδή θα έχουμε δύο διαφορετικά-ισομερή αλκάνια. Το n-βουτάνιο και το ισοβουτάνιο (μέθυλο προπάνιο).
Με πέντε άτομα έχουμε τρεις διαφορετικές διατάξεις:
 |  | |
| n-Πεντάνιο | Ισοπεντάνιο | Νεοπεντάνιο |
που σύμφωνα με την ονοματολογία της IUPAC ονομάζονται πεντάνο. μέθυλοβουτάνιο και διμέθυλοπροπάνιο και έχουν όλα τον ίδιο μοριακό τύπο C5H12
Με έξι άτομα άνθρακα και τα απαραίτητα υδρογόνα φτιάχνουμε πέντε διαφορετικά ισομερή, ενώ με επτά εννιά και με οκτώ δεκαοκτώ.
Το πρόβλημα των πόσων ισομερών αλκανίων θα έχουμε με n άνθρακες είναι ένα μαθηματικό πρόβλημα που δεν εμφανίζει κάποια απλή κανονικότητα. Δεν υπάρχει κάποιος μαθηματικός τύπος. Έτσι τα δέντρα που κατασκευάζονται με n-τετραπλούς κόμβους (από κάθε κόμβο να ξεκινάνε τέσσερα κλαδιά) σύμφωνα με την "On-Line Encyclopedia of Integer Sequences" είναι : 1, 1, 1, 2, 3, 5, 9, 18, 35, 75, 159, 355, 802, 1858, 4347, 10359, 24894, 60523, 148284, 366319, 910726, 2278658, 5731580, 14490245, 36797588, 93839412, 240215803, 617105614, 1590507121, 4111846763, 10660307791, 27711253769.
Δηλαδή το τριαντάνιο έχει περίπου 4,1 δισεκατομμύρια ισομερή και
το τριανταδιάνιο 27,7 δισεκατομμύρια,
ενώ το εξηντάνιο έχει 22158734535770411074184 δηλαδή 2,2*1022 διαφορετικά ισομερή.
Και τέλος το εκατονεξηνταεπτάνιο C167H336 έχει τόσα ισομερή όσα όλα τα σωματίδια του σύμπαντος σύμφωνα με το άρθρο των Robert E. Davies, and Peter J. Freyd με τίτλο: C_{167}H_{336} is The Smallest Alkane with More Realizable Isomers than the Observable Universe has Particles, Journal of Chemical Education, Vol. 66, 1989, pp. 278-281. που μπορείτε να βρείτε στο:
https://pubs.acs.org/doi/pdfplus/10.1021/ed066p278
Και τέλος το εκατονεξηνταεπτάνιο C167H336 έχει τόσα ισομερή όσα όλα τα σωματίδια του σύμπαντος σύμφωνα με το άρθρο των Robert E. Davies, and Peter J. Freyd με τίτλο: C_{167}H_{336} is The Smallest Alkane with More Realizable Isomers than the Observable Universe has Particles, Journal of Chemical Education, Vol. 66, 1989, pp. 278-281. που μπορείτε να βρείτε στο:
https://pubs.acs.org/doi/pdfplus/10.1021/ed066p278
| Number of n-node unrooted quartic trees; number of n-carbon alkanes C(n)H(2n+2) ignoring stereoisomers. Για τους τριάντα δύο πρώτους ακέραιους οι τιμές είναι στη σελίδα https://oeis.org/A000602 από τον N. J. A. Sloane |
| 1 | 1 | |
| 2 | 1 | |
| 3 | 1 | |
| 4 | 2 | |
| 5 | 3 | |
| 6 | 5 | |
| 7 | 9 | |
| 8 | 18 | |
| 9 | 35 | |
| 10 | 75 | |
| 11 | 159 | |
| 12 | 355 | |
| 13 | 802 | |
| 14 | 1858 | |
| 15 | 4347 | |
| 16 | 10359 | |
| 17 | 24894 | |
| 18 | 60523 | |
| 19 | 148284 | |
| 20 | 366319 | |
| 21 | 910726 | |
| 22 | 2278658 | |
| 23 | 5731580 | |
| 24 | 14490245 | |
| 25 | 36797588 | |
| 26 | 93839412 | |
| 27 | 240215803 | |
| 28 | 617105614 | |
| 29 | 1590507121 | |
| 30 | 4111846763 | |
| 31 | 10660307791 | |
| 32 | 27711253769 |
Αν ενδιαφέρεστε για μέχρι τους 60 άνθρακες θα τα βρείτε εδώ: https://oeis.org/A000602/b000602.txt επίσης από τον N. J. A. Sloane
Και τέλος στη σελίδα https://oeis.org/A000602/a000602_1.txt μπορείτε να βρείτε ένα πρόγραμμα για τον υπολογιστή σας, από τον Jean-François Alcover, που σας δίνει αυτές τις ακολουθίες. Το πρόγραμμα είναι γραμμένο στη γλώσσα mathematica (γλώσσα μαθηματικών από το MIT) και μπορείτε να το εκτελέσετε στο cloud από εδώ: http://develop.open.wolframcloud.com/app/
Πηγή: "On-Line Encyclopedia of Integer Sequences"